FD集的最小依赖集

定义4.7  如果关系模式R（U）上的两个函数依赖集F和G，有F+=G+，则称F和G是等价的函数依赖集。
（两个函数依赖集F和G等价的充分必要条件是F＋＝G＋）

定义4.8  设F是属性集U上的FD集。如果Fmin是F的一个最小依赖集，那么Fmin应满足下列四个条件：
⑴ F+min =F+；
⑵ 每个FD的右边都是单属性；
⑶ Fmin中没有冗余的FD（即F中不存在这样的函数依赖X→Y，使得Fmin与Fmin －｛ X→Y ｝等价）（即这个函数依赖的存在不会影响函数依赖集，就把它去掉）；
⑷ 每个FD的左边没有冗余的属性（即Fmin中不存在这样的函数依赖X→Y，X有真子集W使得Fmin －｛ X→Y ｝∪｛ W→Y ｝与Fmin等价）。(即左边X的真子集W能够推出Y时，就不要X　Y，直接取W　Y)

例4.8  设F是关系模式R（ABC）的FD集，F=｛ A→BC，B→C，A→B，AB→C ｝，试求Fmin。
① 先把F中的FD写成右边是单属性形式：
F=｛ A→B，A→C，B→C，A→B，AB→C ｝
显然多了一个A→B，可删去。得F=｛ A→B，A→C，B→C，AB→C ｝

② F中AB→C可从A→B和B→C通过A3、A7原则推出(或者B为AB的真子集， B→C，那么根据最小依赖集定义（4）可知AB→C为左边有冗余的属性，可以去掉，保留B→C即可)，因此AB→C也可删去。

③ F中A→C可从A→B和B→C推出，因此A→C是冗余的，可删去。最后得F=｛ A→B，B→C ｝，即所求的Fmin。 

计算函数依赖集F的最小依赖集G。
具体过程分为三步：
（1）据推理规则的分解性A5，得到一个与F等价的FD集G，G中的每个FD的右边均为单属性。
（2）在G的每个FD中消除左边冗余的属性
（3）在G中消除冗余的FD
上述算法中，操作步骤的顺序很重要，不能颠倒。颠倒了就有可能消除不了FD冗余的属性。但是如果2中没有冗余的属性可以跳到第3步去执行。

模式分解问题

定义4.9  设有关系模式R(U)，属性集为U，R1、…、Rk都是U的子集，并且有R1∪R2∪…∪Rk＝U。关系模式R1、…、Rk的集合用ρ表示，ρ=｛R1，…，Rk｝。用ρ代替R的过程称为关系模式的分解。这里ρ称为R的一个分解，也称为数据库模式。

一般把上述的R称为泛关系模式（P42），R对应的当前值称为泛关系（P43）。数据库模式ρ对应的当前值称为数据库实例，它是由数据库模式中的每一个关系模式的当前值组成，用σ=<r1, … , rk>表示。

模式分解示意图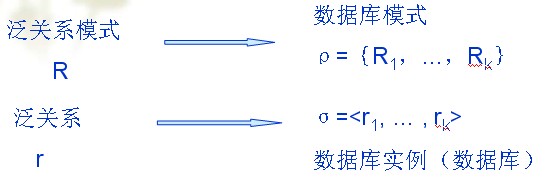

因此，在计算机中数据并不是存储在泛关系r中，而是存储在数据库σ中。那么，就会产生两个问题：
①σ和r是否等价，即是否表示同样的数据。这个问题用“无损分解”特性表示。
②在模式R上有一个FD集F，在ρ的每一个模式Ri上有一个FD集Fi，那么｛F1， … ，Fk｝与F是否等价。这个问题用“保持依赖”特性表示。Npe:N2